Розуміння статистики, яку використовують казино, має важливе значення для оцінки результатів. Ми використовуємо це, щоб визначити, чи результати, погані чи хороші, є функцією удачі чи навичок.
Тут я застосую статистичний аналіз до блекджеку, але з мінімальними зусиллями це можна застосувати до будь-якої гри в казино novosobor.dp.ua.
Блекджек не дотримується традиційних математичних законів гри. Більшість азартних ігор відображають математичну концепцію, відому як «закон незалежних випробувань», яка стверджує, що минулі події не мають відношення до майбутніх подій.
Якщо підкинути монету, є 50% ймовірність того, що результат буде орлом, і 50% ймовірність того, що результат буде решкою. Якщо монета випаде 10 голів поспіль, то наступне підкидання знову матиме 50% ймовірність випадання голів. У блекджеку те, що відбувається в минулому, безпосередньо впливає на те, що відбувається в майбутньому. Блекджек має пам’ять, і закон незалежних випробувань не діє.
Погляд на переваги
У блекджеку кожна карта має певне значення, яке вона додає або віднімає від початкової переваги, яку казино має над гравцем. Коли роздається достатня кількість правильних карт, перевага змінюється на користь гравців.
У блекджеку, коли роздається туз або карта номіналом 10, перевага казино над гравцем збільшується. Коли в гру вводяться карти меншої вартості, перевага казино зменшується, а коли роздається достатня кількість цих карт, гравець отримує перевагу над казино.
Коли залишається велика кількість високих карт, гравець отримує перевагу перед казино. Це відбувається з кількох причин. По-перше, блекджек роздають частіше, і оскільки виграш у блекджеку є асиметричним (гравець отримує виплату 3:2 у блекджеку гравця, але програє свою початкову ставку лише у блекджеку дилера), це вигідно гравцеві.
По-друге, деякі параметри гравця стають більш цінними, наприклад розділення та подвоєння. Зазвичай гравець хоче, щоб старша карта вийшла під час подвоєння чи розбиття, або гравець застосовує ці варіанти, коли дилер слабкий, а висока карта, ймовірно, зламає дилера.
Ці ігри мають вищий прибуток, коли колода багата високими картами. Нарешті, гравець може змінювати свою стратегію залежно від складу карт, що залишилися. З переважанням високих карт гравець може стояти на більш жорстких руках (загальна сума 12-16), частіше подвоюватися з сильними підсумками або коли дилер слабкий і сприйнятливий до перевищення 21. Навпаки, правила забороняють дилера від зміни його стратегії.
Всередині чисел
Стратегія, яка дає перевагу в 1%, означає, що для кожної роздачі блекджеку, зіграної за 100 доларів, очікувана вартість становить 1 долар. Це обчислюється за рівнянням очікуваного значення в рівнянні 1.
EV = РОЗМІР СТАВКИ (X) % ПЕРЕВАГИ (X) КІЛЬКІСТЬ ЗІГРАНИХ РОЗДАЧ
Рівняння 1
Якщо ми застосуємо сценарій очікуваної вартості до підкидання монети, ми знаємо, що у монети дві сторони, тож ми маємо 50% ймовірність приземлитися орлами та 50% ймовірністю приземлитися решкою, тому рівняння для того, скільки олів ми розрахунок на 100 кидків монети міститься в рівнянні 2. Це рівняння з однією змінною, і розмір ставки можна встановити рівним 1.
EV= ½ (X) 100
Рівняння 2
Коли монету підкидають 100 разів, результат рідко буває рівно 50 орлами і 50 решками. Тому ми повинні ввести поняття дисперсії на кількість подій. Дисперсія є мірою статистичної дисперсії. Говорячи простою мовою, це стосується того, наскільки далеким від очікуваного значення може бути результат випробування чи експерименту.
Дотримуючись прикладу підкидання монети, дисперсія допомагає відповісти на запитання, чи було б несподіваним, якби ми спостерігали 45 голів зі 100 випробувань, чи спостерігали лише п’ять голів у 100 підкиданнях монет. Відповіді ні та так. Отримання лише п’яти голів за 100 підкидань монети фактично означає, що ви підкинули зважену монету.
Розуміння цієї концепції має вирішальне значення, оскільки потрібен належний статистичний аналіз, щоб визначити, чи результати команди (хороші, чи погані) є функцією удачі, чи майстерності.
Погляд на дисперсію
Дисперсію зазвичай обговорюють у термінах стандартних відхилень, і так буде й далі в цьому обговоренні. Стандартне відхилення – це просто квадратний корінь із дисперсії. Стандартне відхилення для серії випробувань визначається рівнянням 3.
Cтанд. Відхилення = (Стандартне відхилення для однієї події) X (Кількість подій)^(1/2)
Рівняння 3
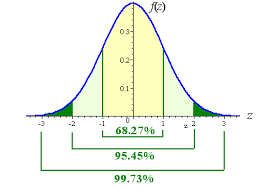
На наступному малюнку показано, наскільки ймовірно, що результати будуть знаходитися в межах одного, двох і трьох стандартних відхилень від очікуваного результату. У графічному зображенні очікуване значення позначається грецькою літерою MU, а стандартне відхилення – грецькою літерою SIGMA.
Відповідно до кривої розподілу Гаусса існує трохи більше 68% ймовірності того, що результат буде в межах одного стандартного відхилення плюс або мінус очікуваного значення. Імовірність того, що результати будуть в межах двох стандартних відхилень плюс або мінус очікуваного значення, становить трохи більше 95%. Існує приблизно 100% ймовірність того, що результати будуть в межах трьох стандартних відхилень у будь-який момент часу.
Застосовуючи це до сценарію 100 підкидань монети, ми приходимо до висновку, що стандартне відхилення для 100 випробувань у 10 разів перевищує стандартне відхилення для одного випробування (що становить 0,5), що дає стандартне відхилення 5 для 100 пробного експерименту.
У сценарії підкидання монети ми очікуємо, що 50 зі 100 підкидань припадуть на орлов, а 50 зі 100 — на решку. Враховуючи концепцію стандартного відхилення плюс-мінус 5, існує 68% ймовірність того, що при 100 підкиданнях монети монета впаде десь між 45 і 55 орлами та решками.
Застосовуючи рівняння очікуваної вартості та стандартного відхилення до одиниці ставок у 100 доларів із загальною перевагою в 1%, обчислюються наступні результати.
| Кількість рук | Очікуване значення | Стандартне відхилення |
| 100 | 100 |
|
| 10 000 | 10 000 |
|
| 1 000 000 | 1 000 000 |
|
Графічно це зображується наступним чином.
Зі збільшенням кількості подій стандартне відхилення стає все меншим і меншим відносно очікуваного значення. У деякій точці кривої очікуване значення та стандартне відхилення перетинаються.
У цей момент існує 84% ймовірність того, що стандартне відхилення буде меншим за очікуване значення. Це дає 84% ймовірність отримання прибутку. Коли кількість подій перевищує цю точку, відсоток збільшується логарифмічно. Це графічно показано на наступному графіку.
ДЛЯ ПРОСТОТИ ЗНАЧЕННЯ СТАНДАРТНОГО ВІДХИЛЕННЯ Є АБСОЛЮТНИМ
Точка перетину між очікуваним значенням і стандартним відхиленням знаходиться трохи нижче 12 000 рук. При 12 000 роздачах існує 84% ймовірність того, що очікуване значення перевищить негативне стандартне відхилення, що вказує на позитивне EV у 84% випадків.
Коли загальна перевага збільшується, точка «еквівалентності» або кількість роздач, у яких очікуване значення дорівнює стандартному відхиленню, досягається при меншій кількості роздач. Обчислюючи той самий графік із перевагою 2%, графік показує точку еквівалентності 5600 рук.
ДЛЯ ПРОСТОТИ ЗНАЧЕННЯ СТАНДАРТНОГО ВІДХИЛЕННЯ Є АБСОЛЮТНИМ
Додавання переваги
Найефективніший спосіб збільшити перевагу — мати високий спред ставок. В ідеальному сценарії гравець ставить багато, коли є перевага, і нічого, коли переваги немає.
Уявіть собі гру, де коли монета підкидається і коли вона потрапляє на орла, людина отримує 2 одиниці, а коли монета потрапляє на решку, людина має заплатити 1 одиницю. Ви б зіграли в цю гру? Більшість людей скажуть так.
Однак ви повинні переконатися, що у вас достатньо одиниць, щоб подолати будь-які негативні коливання, з якими ви можете зіткнутися. Якби у людини було лише 4 одиниці для ставки, можливо, монета могла впасти на решку 4 рази поспіль, і людина втратила б усі свої кошти. Однак, якби людина мала 100 одиниць, у неї було б достатньо коштів, щоб пережити негативні коливання в грі, і існує дуже хороший шанс, що ця гра буде прибутковою для гравця.
В іграх у казино потрібно достатньо коштів, щоб пережити будь-які негативні коливання, які можуть статися. Загалом, чим більше у вас коштів, тим більше шансів на успіх. Ось чому казино часто переживають гравців, оскільки гравець ніколи не може отримати довготривалий результат і подолати статистичні лежачі поліцейські, які виникають.